1 Point Find the Solution to the Boundary Value Problem
Solution to Boundary Value Problems
A boundary value problem is one in which we specify the traction applied on the surface of a body and/or displacement of the boundary of a body and are interested in finding the displacement and/or the stress at any interior point in the body or on part of the boundary where they were not specified. This specification of the boundary traction and/or displacement is called as boundary condition. The boundary condition is in a sense constitutive relation for the boundary. It tells how the body and its surroundings interact. Thus, in a boundary value problem one needs to prescribe the geometry of the body, the constitutive relation for the material that the body is made up of for the process it is going to be subjected to and the boundary condition. Using this information one needs to find the displacement and stress that the body is subjected to. The so found displacement and stress field should satisfy the equilibrium equations, constitutive relations, compatibility conditions and boundary conditions.
The purpose of formulating and solving a boundary value problem is to:
1. To ensure the stresses are within prescribed limits
2. To ensure that the displacements are within prescribed limits
3. To find the distribution of forces and moments on part of the boundary where displacements are specified
There are four type of boundary conditions. They are
1. Displacement boundary condition:Here the displacement of the entire boundary of the body alone is specified. This is also called as Dirichlet boundary condition
2. Traction boundary condition:Here the traction on the entire boundary of the body alone is specified. This is also called as Neumann boundary condition
3. Mixed boundary condition: Here the displacement is specified on part of the boundary and traction is specified on the remaining part of the boundary. Both traction as well as displacement are not specified over any part of boundary
4. Robin boundary condition:Here both the displacement and the traction are specified on the same part of the boundary.
There are three methods by which the displacement and stress field in the body can be found, satisfying all the required governing equations and the boundary conditions. Outline of these methods are presented next. The choice of a method depends on the type of boundary condition.
Displacement method
Here displacement field is taken as the basic unknown. Then, using the strain displacement relation, (1.14) the strain is computed. This strain in substituted in the constitutive relation, (1.17) to obtain the stress. The stress is then substituted in the equilibrium equation (1.6) to obtain 3 second order partial differential equations in terms of the components of the displacement field as,
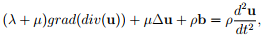
where ∆(�) stands for the Laplace operator and t denotes time. Equation (1.22) is called the Navier-Lam`e equations. Thus, in the displacement method equation (1.22) is solved along with the prescribed boundary condition.
If three dimensional solid elements are used for modeling the body in finite element programs, then the weakened form of equation (1.22) is solved for the specified boundary conditions.
Stress method
In this method, the stress field is assumed such that it satisfies the equilibrium equations as well as the prescribed traction boundary conditions. For example, in the absence of body forces and static equilibrium, it can be easily seen that if the Cartesian components of the stress are derived from a potential, 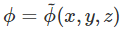
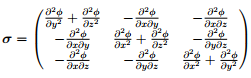
then the equilibrium equations are satisfied. Having arrived at the stress, the strain is computed using
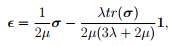
obtained by inverting the constitutive relation, (1.17). In order to be able to find a smooth displacement field from this strain, it has to satisfy compatibility condition (1.15). This procedure is formulated in chapter 7 and is followed to solve some boundary value problems in chapters 8 and 9.
Semi-inverse method
This method is used to solve problems when the constitutive relation is not given by Hooke's law (1.17). When the constitutive relation is not given by Hooke's law, displacement method results in three coupled nonlinear partial differential equations for the displacement components which are difficult to solve. Hence, simplifying assumptions are made for the displacement field, wherein a the displacement field is prescribed but for some constants and/or some functions. Except in cases where the constitutive relation is of the form (1.16), one has to make an assumption on the components of the stress which would be nonzero for this prescribed displacement field. Then, these nonzero components of the stress field is found in terms of the constants and unknown functions in the displacement field. On substituting these stress components in the equilibrium equations and boundary conditions, one obtains differential equations for the unknown functions and algebraic equations to find the unknown constants. The prescription of the displacement field is made in such a way that it results in ordinary differential equations governing the form of the unknown functions. Since part displacement and part stress are prescribed it is called semi-inverse method. This method of solving equations would not be illustrated in this course.
Finally, we say that the boundary value problem is well posed if (1) There exist a displacement and stress field that satisfies the boundary conditions and the governing equations (2) There exist only one such displacement and stress field (3) Small changes in the boundary conditions causes only small changes in the displacement and stress fields. The boundary value problem obtained when Hooke's law (1.17) is used for the constitutive relation is known to be well posed.
1 Point Find the Solution to the Boundary Value Problem
Source: https://edurev.in/studytube/Solution-to-Boundary-Value-Problems-Advanced-Solid/021d2394-9bc0-4c61-b0dc-69973215fafd_t